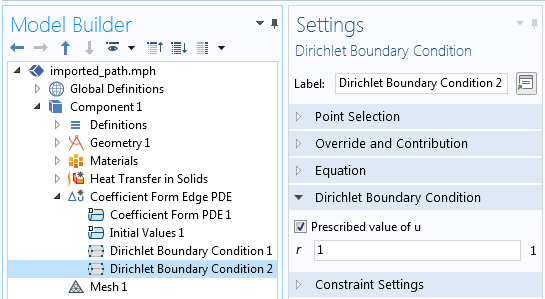
giftowl.blogg.se - Dirichlet boundary condition

#DIRICHLET BOUNDARY CONDITION PLUS#

Which determine the current flux across the interface, must be used. Neumann interface condition, like the TFE model or the TE model, Also theīandgap alignment of the adjustent semiconductors is ignored when suchĬontinuous condition is enforced. However, it is erroneous to assumeĬontinuous quasi- Fermi levels at abrupt heterojunctions. Quasi- Fermi level across the interface remains continuous. The carrier concentrations are directly determined in a way that the Interface and the effective tunneling lengthīy using the CQFL model a Dirichlet interface condition is applied. The barrier height lowering depends on the electric field orthogonal to the Is self-contained and there are no fluxes across the boundary.

The Neumann boundary condition guarantees that the simulation domain In order to separate the simulated device from neighboring devices, artificialīoundaries must be specified which are not boundaries in a physical sense. At theīoundaries of this domain appropriate boundary conditions need to be specified The basic semiconductor equations are posed in a bounded domain.

3.1.6.6.3 Semiconductor-Semiconductor Thermal Interface.

3.1.6.6.2 Thermionic Field Emission Model.

3.1.6.6.1 Continuous Quasi- Fermi Level Model.

3.1.6.6 Semiconductor-Semiconductor Interface.

3.1.6.4 Semiconductor-Insulator Interface.

Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 2-4.Next: 3.2 Lattice and Thermal Up: 3.1 Sets of Partial Previous: 3.1.5 The Insulator Equations Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 3-2. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 9-4. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 3-2. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.

Physics of Nuclear Kinetics. Addison-Wesley Pub. Nuclear and Particle Physics. Clarendon Press 1 edition, 1991, ISBN: 978-0198520467 Nuclear Reactor Engineering: Reactor Systems Engineering, Springer 4th edition, 1994, ISBN: 978-0412985317 Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 8-1. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983). Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Fundamentals of Heat and Mass Transfer. C.

Fundamentals of Heat and Mass Transfer, 7th Edition.

#DIRICHLET BOUNDARY CONDITION PLUS#

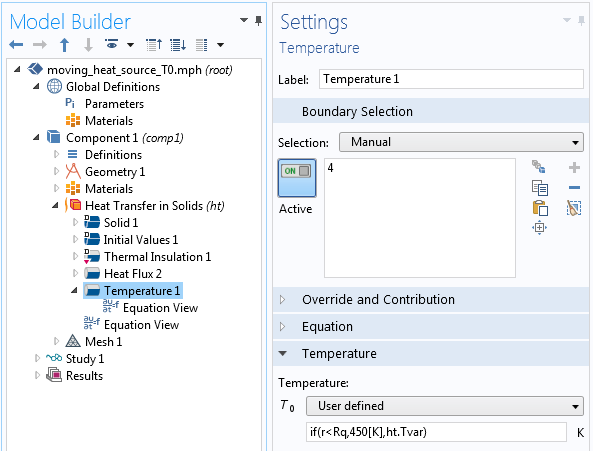
In words, the heat conduction equation states that:Īt any point in the medium the net rate of energy transfer by conduction into a unit volume plus the volumetric rate of thermal energy generation must equal the rate of change of thermal energy stored within the volume. From its solution, we can obtain the temperature field as a function of time. This equation is also known as the Fourier-Biot equation, and provides the basic tool for heat conduction analysis. Using these two equation we can derive the general heat conduction equation: The Fourier’s law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area, at right angles to that gradient, through which the heat flows.Ī change in internal energy per unit volume in the material, ΔQ, is proportional to the change in temperature, Δu. The heat equation is derived from Fourier’s law and conservation of energy. Once this temperature distribution is known, the conduction heat flux at any point in the material or on its surface may be computed from Fourier’s law. Detailed knowledge of the temperature field is very important in thermal conduction through materials. The heat conduction equation is a partial differential equation that describes the distribution of heat (or the temperature field) in a given body over time.